Scipy
wikiによれば
SciPyもpandasと同様にできることが多い。 特殊関数や方程式の数値解法、フーリエ変換、近似曲線、線形代数、微積などが行えるが、 ここでは主に実験データ解析に必要であろう物理定数とデータ補間について説明する。SciPyはPythonのための科学的ツールのオープンソース・ライブラリとして開発されている。 SciPyは配列の高速な操作のためのすべてのライブラリを含んでおり、 人気のNumericモジュールを置き換え、 ひとつのパッケージとして高レベルな科学と工学のモジュールを集めたもの。
SciPyは、配列オブジェクトとその他の基本的な機能を備えたNumPyを基礎にしている。 SciPy は統計、最適化、積分、線形代数、フーリエ変換、 信号・イメージ処理、遺伝的アルゴリズム、ODE (常微分方程式) ソルバ、特殊関数、その他のモジュールを提供する。 Cythonで記述することがある。
物理定数
SciPyはconstantsパッケージ内に物理定数がいろいろ入っている。
[参照] https://docs.scipy.org/doc/scipy/reference/constants.html
from scipy import constants
print('光速', constants.c)
print('プランク定数', constants.h)
print('電気素量', constants.e)
print('ボルツマン定数', constants.k)
print('アボガドロ定数', constants.N_A)
_c_ = (constants.mu_0 * constants.epsilon_0)**(-1/2)
print('1/c^2 = mu_0 x epsilon_0', _c_)
| 定数 | 変数名 | 値 | 単位 |
|---|---|---|---|
| 光速(真空中) | c, speed_of_light | 299792458.0 | m s-1 |
| 磁気定数(真空の透磁率) | mu_0 | 1.25663706212e-06 | N A-2 |
| 電気定数(真空の誘電率) | epsilon_0 | 8.8541878128e-12 | F m-1 |
| プランク定数 | h, Planck | 6.62607015e-34 | J s |
| 換算プランク定数 | hbar | 1.0545718176461565e-34 | J s |
| 重力定数 | G, gravitational_constant | 6.6743e-11 | m3 kg-1 s-2 |
| 標準重力加速度 | g | 9.80665 | m s-2 |
| 電気素量(素電荷、電荷素量) | e, elementary_charge | 1.602176634e-19 | C |
| 気体定数 | R, gas_constant | 8.314462618 | J K-1 mol-1 |
| 微細構造定数 | alpha, fine_structure | 0.0072973525693 | 無次元 |
| アボガドロ定数 | N_A, Avogadro | 6.02214076e+23 | mol-1 |
| ボルツマン定数 | k, Boltzmann | 1.380649e-23 | J K-1 |
| シュテファン=ボルツマン定数 | sigma, Stefan_Boltzmann | 5.670374419e-08 | W m-2 K-4 |
| ウィーンの変位定数 | Wien | 0.002897771955 | m K |
| リュードベリ定数 | Rydberg | 10973731.56816 | m-1 |
| 電子質量 | m_e, electron_mass | 9.1093837015e-31 | kg |
| 陽子質量 | m_p, proton_mass | 1.67262192369e-27 | kg |
| 中性子質量 | m_n, neutron_mass | 1.67492749804e-27 | kg |
上記表の単位は全てSI(MKSA)単位系である(CGS系で使いたいなら単位変換が必要)。
データの補間
サンプルデータ。
測定した実験データの点は離散的であるから 本来はデータ点の間の領域の情報を得ることはできるない。 しかし、領域内に適当な曲線を当てはめることで 測定されたデータ点以外の情報も推定することができるようになる。
例として次のようなデータが測定されたとする。
x = [1, 2, 3, 5], y = [2, 4, 1, 3]
これをプロットしたのが右図である。 測定データとしてマーカーがプロットされた点は測定データであるから \(x=2\to y=4\)などと情報が得られる。 しかし、それ以外の点、例えば\(x=1.5\)や\(x=4\)のときの\(y\)の値は不明である。 これらの値を求めるときに行うのが「補間」あるいは「内挿」である。scipyで補間を行うには"scipy.interpolate"モジュールを用いる。 1変数\(y=f(x)\)での補間であれば、"interp1d"を用いることで補完関数を取得できる。
from scipy import interpolate
import numpy as np
import matplotlib.pyplot as plt
# 観測データ
observed_x = [1, 2, 3, 5]
observed_y = [2, 4, 1, 3]
# 補間関数取得
f = interpolate.interp1d(observed_x, observed_y)
# 連続した新しいxデータ
new_x = np.linspace(min(observed_x), max(observed_x), 100)
# 補間関数にnew_xを代入し、それに対応するyを取得(new_yに代入)
new_y = f(new_x)
print('x=1.5:', f(1.5))
print('x=4.0:', f(4.0))
# プロット
plt.scatter(observed_x, observed_y) # 散布図(観測データ)
plt.plot(new_x, new_y) # 補間曲線
plt.xlabel(r'$x$')
plt.ylabel(r'$y$')
plt.grid()
plt.show()
上記コードで重要なのは10行目であり、 ここで観測されたx,yデータに基づいた補間関数を生成している。 渡せる主なパラメータは以下の通りである。
from scipy import interpolate
f = interpolate.interp1d(
x,
y,
kind = 'linear',
fill_value = nan
)
"kind"では補間の種類を指定できる。 デフォルトでは'liner'が指定されている。 "fill_value"では外挿値を指定できる。 デフォルトではnanが指定されており、外挿しようとするとエラーになる。 (上記コードだとxの範囲が1~5までであり、f(1.5),f(4.0)は内挿に相当する為、 エラーはでないが、f(0)やf(6)はエラーとなる。) 外挿を行いたい場合は、"fill_value"に"extrapolate"を指定することで行える。
from scipy import interpolate
import numpy as np
# 観測データ
observed_x = [1, 2, 3, 5]
observed_y = [2, 4, 1, 3]
# 補間関数取得
f = interpolate.interp1d(
observed_x,
observed_y,
kind = 'linear', # 補間手法をlinearと明示
fill_value = 'extrapolate' # 外挿も行えるように指定
)
print('内挿 x=1.5:', f(1.5))
print('内挿 x=4.0:', f(4.0))
print('外挿 x=0.0:', f(4.0))
print('外挿 x=6.0:', f(6.0))
補間手法
補間手法として、上記例ではデフォルトの'linear'(線形補完)のコードを示した。 scipyでは他にも補間手法が容易されており、それらは以下の通りである。
| 引数名 | 補間方法 |
|---|---|
| linear | 線形補間(デフォルト) |
| nearest | 最近傍補間(切捨) |
| nearest-up | 最近傍補間(切上) |
| zero | 0次スプライン |
| slinear | 1次スプライン |
| quadratic | 2次スプライン |
| cubic | 3次スプライン |
| previous | 前方参照 |
| next | 後方参照 |
import matplotlib.pyplot as plt
import numpy as np
from scipy import interpolate
# 観測データ
x = np.array([0.2, 0.9, 2.2, 2.9, 3.8, 5.1, 6.2])
y = np.array([4.6, 12.5, 6.7, 9.0, 3.4, 5.8, 4.5])
# 補間方法一覧とプロット時のラベルと色指定
KIND_DICT = {
'linear':
{'label': '線形補間', 'color':'orange'},
'nearest':
{'label':'最近傍補間(切捨)', 'color':'blue'},
'nearest-up':
{'label':'最近傍補間(切上)', 'color':'cyan'},
'zero':
{'label':'0次スプライン', 'color':'green'},
'slinear':
{'label':'1次スプライン', 'color':'red'},
'quadratic':
{'label':'2次スプライン', 'color':'purple'},
'cubic':
{'label':'3次スプライン', 'color':'pink'},
'previous':
{'label':'前方参照', 'color':'brown'},
'next':
{'label':'後方参照', 'color':'olive'}
}
# 連続xデータ
new_cont_x = np.linspace(x.min(), x.max(), 100)
# figure作成
fig = plt.figure()
cnt = 1
# KIND_DICT辞書をforで回す
for key in KIND_DICT:
# 補間関数作成
f = interpolate.interp1d(x, y, kind=key, fill_value='extrapolate')
# ax作成
ax = fig.add_subplot(3, 3, cnt)
# 観測データプロット
ax.scatter(x, y, marker='o', c='k')
color = KIND_DICT[key]['color'] # 補間法ごとの色
label = KIND_DICT[key]['label'] # 補間法ごとのラベル
# 補間曲線プロット
ax.plot(new_cont_x , f(new_cont_x), ls='--', c=color, label=label)
ax.legend() # 凡例表示
ax.grid() # グリッド表示
cnt += 1
# 図の余白微調整
fig.tight_layout()
fig.subplots_adjust(wspace=0.15, hspace=0.15)
plt.show()
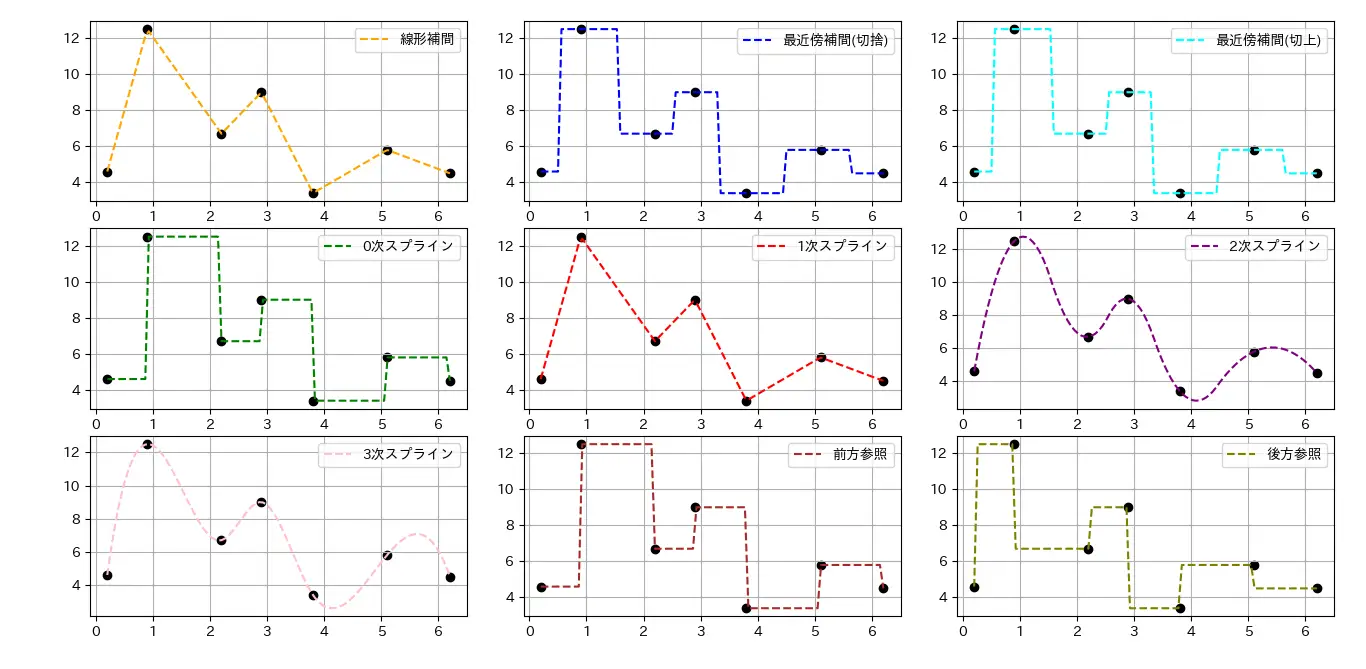
補間法による振舞いの違い
スプライン補間
前任者に作っていただいた実験データ解析プログラムでは補間法として"quadratic"を採用している。 ここではスプライン補間について紹介する。
スプライン補間とはデータを区分ごとに分割し、その区分領域を多項式で表現する方法である。 2点(\(x_{i}, x_{i+1}\))間の補間関数を\(S_i(x)\)と表せば、全体の補間関数\(S(x)\)は \begin{align*} S(x)=\begin{cases} S_0(x)&(x_0\leq x < x_1)\\ S_1(x)&(x_1\leq x < x_2)\\ \vdots\\ S_{N-1}(x)&(x_{N-1}\leq x < x_N) \end{cases} \end{align*} と書ける。ここで\(N\)はデータ点の個数である。
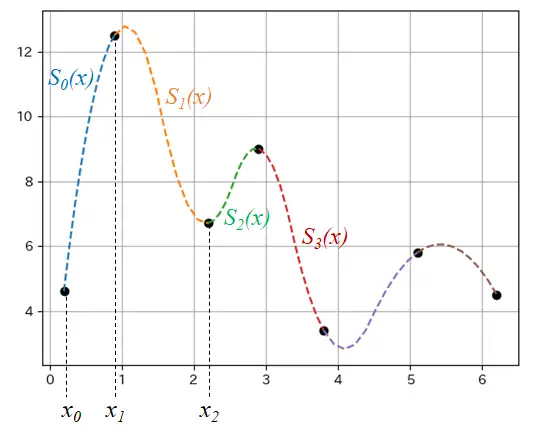
スプライン補間。図は"quadratic"を採用したもの。
\(S_i(x)\)として3次関数\(f(x)=ax^3+bx^2+cx+d\)を採用したものを「3次スプライン補間」と呼び、 2次関数を採用したものを「2次スプライン補間」、1次関数を採用したものを「1次スプライン補間」、 0次関数を採用したものを「0次スプライン補間」と呼ぶ。
3次スプライン補間
3次スプライン補間の場合、関数を決定するには係数\(a,b,c,d\)を求める必要があるが、 スプライン補間では条件として以下を課すという特徴をもつ。
- \(S_i(x)\)はデータ点を通る。 即ち、\(S_i(x_i)=y_i,S_i(x_{i+1})=y_{i+1}\)という条件を満たす。
- データ点にて隣り合う区間の1階微分係数が一致する。 即ち、\({S_i}'(x_i)={S_{i+1}}'(x_i)\)という条件を満たす。
- データ点にて隣り合う区間の2階微分係数が一致する。 即ち、\({S_i}''(x_i)={S_{i+1}}''(x_i)\)という条件を満たす。
3次スプライン補間がよく使われるらしく、これに関してはネットでもテキストが見つかる。 前任者のコードでは"quadratic"(2次スプライン補間)が使われているので これにもう少し詳しく見ていく
2次スプライン補間
2次スプライン補間の条件は以下である。
- \(S_i(x)\)はデータ点を通る。 即ち、\(S_i(x_i)=y_i,S_i(x_{i+1})=y_{i+1}\)という条件を満たす。
- データ点にて隣り合う区間の1階微分係数が一致する。 即ち、\({S_i}'(x_i)={S_{i+1}}'(x_i)\)という条件を満たす。
条件(1)の\(S_i(x_i)=y_i\)より\(N\)個の条件式と \(S_i(x_{i+1})=y_{i+1}\)より\(N-2\)個の条件式が出てくる。 また、条件(2)の\({S_i}'(x_i)={S_{i+1}}'(x_i)\)より\(N-2\)個の条件式が出てくる。 よって、\(N+N-2+N-2=(3N-4)\)個の条件式を得る。 必要な条件式の個数は\(3(N-1)\)個であったから1つ足りないことになる。
※さて、分からないのがここのあと1つの条件である。 ネットの海を漂い、2次スプライン補間について書かれたものを見ると、 最後の条件として左端のデータ点で2階微分係数が0というものを見つけた。 [https://engcourses-uofa.ca/books/numericalanalysis/piecewise-interpolation/quadratic-spline-interpolation/] (3次スプラインについては大量の文献が見つかるのに、 2次スプラインについて書かれたものがほとんどない。) つまり、\(a_0=0\)であるから\(S_0(x)=b_0x+c_0\)となり、 一番左の領域は直線で描かれることになる。 うーん。Scipyだとなっていないですね。 何かしらもう1つ条件式が欲しいのだが、それが分からない。 Scipyの元のコードをみれば分かるのだろうか。 おそらくFortranで書かれてそうなので読みたくない。 というより、"quadratic"のグラフを見るとどうも2次関数には見えない領域がある。 両端だけ2次関数でそれ以外は3次関数で補間してるとかありそう…。
0次・1次スプライン補間
1次スプライン補間は\(S_i(x)=a_ix+b_i\)の直線での補間であるから、これは線形補間に等しい。 また、0次スプライン補間は定数値での補間となりScipyでは前方参照と同じ結果となる。
特殊関数
scipy.specialパッケージ内に特殊関数がいろいろ入っている。
[参照] https://docs.scipy.org/doc/scipy/reference/special.html
詳しくは上記の公式ページを参照。 ここではガンマ関数を紹介して終わる。 ガンマ関数は階乗を拡張した表現で \begin{align} \Gamma(x)=\int_{0}^{\infty}t^{x-1}e^{-t}dt \end{align} で書ける。
from scipy.special import gamma
import numpy as np
import matplotlib.pyplot as plt
def factorial(n):
if n == 0:
return 1
relust = n
for x in range(n-1, 0, -1):
relust *= x
return relust
print(gamma(4))
print(gamma(1/2), np.pi**(1/2)) # piの平方根と等しい
x = np.linspace(0, 10, 100)
n = np.arange(0, 10)
np_factorial = np.frompyfunc(factorial, 1, 1)
y1 = np_factorial(n)
y2 = gamma(x+1)
fig, ax = plt.subplots()
ax.plot(x, y2, c='b')
ax.scatter(n, y1, c='r')
ax.set_yscale('log')
plt.show()
上記コードでは試したないがgamma()は負の領域でも使えるので グラフ化してみると面白しろいかもしれない。
微分・積分
数値微分及び数値積分ができるので紹介しておく。
from scipy.misc import derivative
import numpy as np
import matplotlib.pyplot as plt
def func1(x):
return (x+3) * (x-1) * (x-4)
x = np.linspace(-4, 5, 100)
# x=3における1階微分係数
_X_ = 3
a1 = derivative(func1, _X_, dx=1e-5, n=1)
# y切片計算
a0 = func1(_X_) - a1 * _X_
# 接線
y = a1*x + a0
fig, ax = plt.subplots()
ax.plot(x, func1(x), c='b')
ax.plot(x, y, c='r')
ax.set_xlim(-4, 5)
plt.show()
次に定積分の紹介上記のfunc1と同じ関数を-3から3の範囲で積分している。
import numpy as np
from scipy import integrate
import matplotlib.pyplot as plt
def func1(x):
return (x+3) * (x-1) * (x-4)
x = np.linspace(-4, 5, 100)
print(integrate.quad(func1, -3, 3))
fig, ax = plt.subplots()
ax.plot(x, func1(x), c='b')
x_ = np.linspace(-3, 3, 100)
ax.fill_between(x_, func1(x_), 0, facecolor='lime', alpha=0.5)
ax.set_xlim(-4, 5)
ax.grid()
plt.show()
積分範囲に無限大(np.inf)の指定もできる。 折角なのでガンマ関数を実装してみる。
import numpy as np
from scipy import integrate
from scipy.special import gamma
import matplotlib.pyplot as plt
def func2(t, x):
return t**(x-1) * np.exp(-t)
# Gamma(5) = 4! の計算
print(integrate.quad(func2, 0, np.inf, args=5)) # 下限:0、上限:無限の積分
print(integrate.quad(func2, 0, 1e+4, args=5)) # 下限:0、上限:10^4の積分
# Gamma(1/2)の計算
print(integrate.quad(func2, 0, np.inf, args=1/2))
print(integrate.quad(func2, 0, 1e+3, args=1/2)) # 下限:0、上限:10^3の積分
print('root pi = ', np.pi**(1/2))
def myGamma_upinf(x):
return integrate.quad(func2, 0, np.inf, args=x)[0]
def myGamma_upnum(x):
return integrate.quad(func2, 0, 1e+4, args=x)[0]
# ユニバーサル関数に変換
np_myGamma1 = np.frompyfunc(myGamma_upinf, 1, 1)
np_myGamma2 = np.frompyfunc(myGamma_upnum, 1, 1)
x = np.linspace(1, 10, 1000)
fig = plt.figure()
ax1 = fig.add_subplot(121)
ax1.set_title('Gamma Function')
ax1.plot(x, gamma(x), c='b', label='scipy')
ax1.plot(x, np_myGamma1(x), ls='--', c='r', label='upper limit oo')
ax1.plot(x, np_myGamma2(x), ls='--', c='g', label='upper limit 1e+4')
ax1.set_yscale('log')
ax1.legend()
ax2 = fig.add_subplot(122)
ax2.set_title(r'My $\Gamma$ / SciPy $\Gamma$')
ax2.plot(x, np_myGamma1(x)/gamma(x), c='r', label='upper limit oo')
ax2.plot(x, np_myGamma2(x)/gamma(x), c='g', label='upper limit 1e+4')
ax2.legend()
plt.show()
方程式の数値解
用いるのはoptimize.fsolve(func, x0)
import numpy as np
from scipy.optimize import fsolve
import matplotlib.pyplot as plt
def f(x):
return x
def g(x):
return np.cos(x)
def h(x):
return f(x) - g(x)
p = fsolve(h, 0) #0近傍から解を探す
print('交点p', p)
print('f(p)', f(p))
print('g(p)', g(p))
x = np.linspace(0, 3, 50)
fig = plt.figure()
ax1 = fig.add_subplot(111)
ax1.plot(x, f(x))
ax1.plot(x, g(x))
ax1.scatter(p, f(p), color='g')
plt.show()
交点が複数個ある場合はfsolveの引数x0にリストで複数の初期値を渡すと上手くいく。
import numpy as np
from scipy.optimize import fsolve
import matplotlib.pyplot as plt
def f(x):
return x + 2
def g(x):
return x**2
def h(x):
return f(x) - g(x)
p = fsolve(h, [0, 1]) #0と1近傍から解を探す(2個の解が出る)
print('交点p', p)
print('f(p)', f(p))
print('g(p)', g(p))
x = np.linspace(-2, 3, 50)
fig = plt.figure()
ax1 = fig.add_subplot(111)
ax1.plot(x, f(x))
ax1.plot(x, g(x))
ax1.scatter(p, f(p), color='g')
plt.show()
