Python 入門 練習問題
[1] 条件分岐
Q1. 入園料計算
あるテーマパークの入場料は原則、大学生以上:1,500円、小学生~高校生:1,200円、未就学児:無料(2人まで)となっている。 未就学児が3人以上の場合は3人目から一人あたり1,000円が追加される。 しかし、団体割引として6人以上(未就学児も含む)での申込みの場合は合計額が1割引きとなる。
上記の設定で、大学生以上の人数、小学生~高校生の人数、未就学児の人数を入力すると 入場料の合計が表示されるプログラム。 スクリプトファイル名は「clac_entry.py」とする。 コマンドプロンプトでの動作例は下記に記す。
C:\XXX>python clac_entry.py
大学生以上の人数>2
小~高校生の人数>1
未就学児の人数>1
入場料(円): 4200
C:\XXX>python clac_entry.py
大学生以上の人数>2
小~高校生の人数>0
未就学児の人数>3
入場料(円): 4000
C:\XXX>python clac_entry.py
大学生以上の人数>2
小~高校生の人数>1
未就学児の人数>3
入場料(円): 4680 (団体割引適用)
[発展] 上記のプログラムだと未就学児だけでの入場も可能となっているが、これを禁止したい。 未就学児が入場する場合には必ず大学生以上の同伴が1人以上必要とし、これを出力に反映させたい。
C:\XXX>python clac_entry.py
大学生以上の人数>0
小~高校生の人数>1
未就学児の人数>3
入場不可。大学生以上の同伴者が必要です。
Q2. 和暦<->西暦変換プログラム
Q2.1 西暦 -> 和暦変換プログラム仕様
西暦を入力すると、それに対応した和暦が出力されるプログラム。 サポートする元号は「令和」、「平成」、「昭和」の3つでよい。 令和1年は西暦2019年、平成1年は西暦1989年、昭和1年は西暦1926年からとなるが、 "1年"の場合は"元年"と出力させる。 スクリプトファイル名は「changeYear_western2japan.py」とする。 コマンドプロンプトでの動作例は下記に記す。
C:\XXX>python changeYear_western2japan.py
西暦入力 >2020
令和2年
C:\XXX>python changeYear_western2japan.py
西暦入力 >2000
平成12年
C:\XXX>python changeYear_western2japan.py
西暦入力 >2019
令和元年
Q2.2 和暦 -> 西暦変換プログラム仕様
和暦を入力すると、それに対応した西暦が出力されるプログラム。 受け付ける入力は"R02"、"H13"のような頭文字の大文字アルファベットが元号を表し、 その後に0埋めした年数が続くものとする。 元号を示すアルファベットは令和なら"R"、平成なら"H"、昭和なら"S"とする。 スクリプトファイル名は「changeYear_japan2western.py」とする。 動作例は下記に記す。
C:\XXX>changeYear_japan2western.py
和暦入力 >S40
1965
C:\XXX>changeYear_japan2western.py
和暦入力 >H15
2003
C:\XXX>changeYear_japan2western.py
和暦入力 >R01
2019
Q2.3 入学・卒業年度計算プログラム仕様
生年月を入力すると、高等学校と大学の各入学・卒業年度が出力されるプログラム。 入力は西暦表示とし、"2000/06"などの"YYYY/MM"形式の入力を受け付けるものとする。 小学校には4月1日の時点で満6歳になっている子どもが入学するとし、その後は小学校には6年間、中学校には3年間、高等学校には3年間在籍する。大学は4年制のものとし、浪人や留年は考えない。出力は西暦と和暦の両方で表示させる。 スクリプトファイル名は「calc_admission_graduate_year.py」とする。動作例は下記に記す。
C:\XXX>python calc_admission_graduate_year.py
生年月入力 >1998/06
西暦 和暦
生年月:1998年6月 平成10年6月
高等学校
入学: 2014年4月 平成26年4月
卒業: 2017年3月 平成29年3月
大学
入学: 2017年4月 平成29年4月
卒業: 2021年3月 令和3年3月
[発展] 大学受験時に浪人した場合と大学で留年した場合も考慮したい。 受け付ける入力を生年月だけでなく、浪人年数と留年年数も追加し、 大学入学年度と卒業年度を計算するようにせよ。 下記動作例は浪人はしなかったが、大学時代に1年間留年した場合のもの。
C:\XXX>python calc_admission_graduate_year.py
生年月入力 >1998/06
大学受験時の浪人年数>0
大学時代の留年年数>1
西暦 和暦
生年月:1998年6月 平成10年6月
高等学校
入学: 2014年4月 平成26年4月
卒業: 2017年3月 平成29年3月
大学
入学: 2017年4月 平成29年4月
卒業: 2022年3月 令和4年3月
[2] 繰り返し
Q1. 相関係数計算プログラム
Q1.1 相関係数計算プログラム仕様
2つのリストAとBがあり、それぞれに格納されている値は以下の通りである。
- A = [64, 54, 89, 76, 55, 80, 79, 95, 69, 72]
- B = [76, 89, 92, 69, 84, 79, 84, 83, 91, 75]
※Pythonには組み込み関数sum(リスト)で総和が求まり、len(リスト)でリストの要素数が求まる為、 sum(リスト)/len(リスト)で平均が求まるが、ここでは学習の為これらの組み込み関数は用いずに 上記プログラムを実装してみよ。 なお、分散\({\sigma_A}^2,{\sigma_B}^2\)、共分散\({\sigma_{AB}}^2\)、相関係数\(R\)は以下で定義される。 \begin{align*} {\sigma_A}^2=\frac{1}{n}\sum_{i=1}^{n}(A_i-\langle A \rangle)^2,\quad {\sigma_{AB}}^2=\frac{1}{n}\sum_{i=1}^{n}(A_i-\langle A \rangle)(B_i-\langle B \rangle),\quad R = \frac{{\sigma_{AB}}^2}{\sigma_A\sigma_B} \end{align*} ここで\(\langle X \rangle\)は平均を表す。
C:\XXX>python calc_correl.py
A
総和: 733
平均: 73.3
分散: 161.60999999999999
標準偏差: 12.712592182556632
B
総和: 822
平均: 82.2
分散: 50.160000000000004
標準偏差: 7.0823724838503095
A-B
共分散: -1.05999999999999
相関係数: -0.011773158373432542
Q2. 数列計算プログラム
Q2.1 群数列プログラム仕様
「1, 2, 2, 3, 3, 3, 4, …」という数列を実装したい。 この数列のn番目の項とそこまでの総和を表示するプログラムを書け。 nはinput()関数で入力するものとする。 スクリプトファイル名は「calc_sequence.py」とする。動作例は下記に記す。
C:\XXX>python calc_sequence.py
項数n>5
[1, 2, 2, 3, 3]
11
C:\XXX>python calc_sequence.py
項数n>10
[1, 2, 2, 3, 3, 3, 4, 4, 4, 4]
30
Q3. 最大公約数・最小公倍数計算プログラム
Q3.1 最大公約数プログラム仕様
入力として2つの整数を受け取り、その2数の最大公約数(GCD:greatest common divisor)を出力するプログラム。 スクリプトファイル名は「calc_gcd.py」とする。動作例は下記に記す。
C:\XXX>python calc_gcd.py
a入力 >54
b入力 >126
18
C:\XXX>python calc_gcd.py
a入力 >365664
b入力 >25116
156
Q3.2 最小公倍数プログラム仕様
入力として2つの整数を受け取り、その2数の最小公倍数(LCM:leastcommon multiple)を出力するプログラム。 スクリプトファイル名は「calc_lcm.py」とする。動作例は下記に記す。
C:\XXX>python calc_lcm.py
a入力 >14
b入力 >66
462
C:\XXX>python calc_lcm.py
a入力 >2022
b入力 >614
620754
[発展]GCD・LCMのプログラムはともに2つの入力しか考えなかったが、 入力を1つ増やし3つの数のGCD・LCMを求めるにはどうすれば良いか。 さらに任意個の整数を入力に受け取りそれらのGCD・LCMを求めるプログラムを書け。
Q3. 素数判定プログラム
Q3.1 素数判定プログラム仕様
入力された数値が素数ならTrueを出力し、そうでないならFalseを出力するプログラム。 素数は1とその数以外で割り切れない自然数であり、2,3,5,7,11,…などである。 スクリプトファイル名は「check_prime.py」とする。動作例は下記に記す。
C:\XXX>python check_prime.py
整数入力 > 123
False
C:\XXX>python check_prime.py
整数入力 > 127
True
Q3.2 素因数分解プログラム仕様
入力された整数を素因数分解するプログラム。 例えば、126を素因数分解すると\(126=2\times3^2\times7\)となるが、 このような処理を行うプログラムを作りたい。
入力として整数を受け取り、それの素因数が格納されたリストを表示せよ。 126の例なら、出力されるリストは[2, 3, 3, 7]となる。 スクリプトファイル名は「prime_factorization.py」とする。動作例は下記に記す。
C:\XXX>python prime_factorization.py
整数入力 >126
[2, 3, 3, 7]
C:\XXX>python prime_factorization.py
整数入力 >3120
[2, 2, 2, 2, 3, 5, 13]
[発展]出力するリストの形式を[(素数1, 指数1), (素数2, 指数2), …]としたい。 入力が3120ならその結果は[(2, 4), (3, 1), (5, 1), (13, 1)]となるようにせよ。 また、出力として"3120 = 2^4 x 3 x 5 x 13"が表示されるとなおよい。
Q4. ソートプログラム
Q4.1 バブルソートプログラム仕様
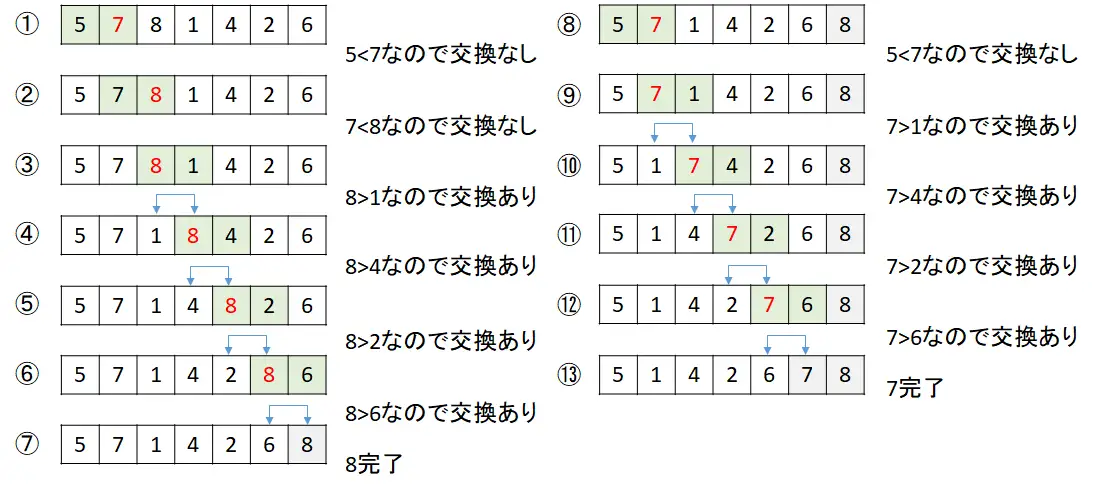
バブルソート
[3] ファイル入出力
Q1. csv(Comma Separated Value)形式ファイルの解析
30名の数学、英語、理科、社会、国語の得点が保存された テキストファイル「sample_data1.txt」について 以下のプログラムを作成してみよう。
Q1.1 理数高得点者検索プログラム仕様
数学と理科の得点がともに90点を超える生徒の一覧を取得し、その結果を「math_sci_good_students_list.txt」に保存したい。 スクリプトファイル名は「write_math_sci_good_students.py」とする。
Q1.2 得点優秀者検索プログラム仕様
得点が90点を超える科目が3つ以上ある生徒の一覧を取得し、その結果を「excellent_students_list.txt」に保存したい。 スクリプトファイル名は「write_excellent_students.py」とする。
[発展]得点のしきい値を90点ではなく、各教科の平均点プラス10点とする場合にはどうすればよいだろうか。
Q1.3 合計・平均計算プログラム仕様
列に対する合計と平均および行に対する合計と平均を計算し、 その結果をテキストファイル「sample_data1_result.txt」として出力せよ。
「sample_data1_result.txt」は以下のような結果を保存するようにせよ。
| id | 氏名 | class | 数学 | 英語 | 理科 | 社会 | 国語 | 合計 | 平均 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 相川 | A | 89 | 85 | 72 | 75 | 90 | 411 | 82.2 |
| 2 | 蒼井 | A | 88 | 74 | 96 | 78 | 74 | 410 | 82.0 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| 合計 | 2481 | ? | ? | ? | ? | ? | ? | ||
| 平均 | 82.7 | ? | ? | ? | ? | ? | ? |
[4] 関数
Q1. 処理の関数化
Q1.1 入園料計算の関数化
[1]Q1で入園料の計算を行うプログラムを書いたが、これを関数化したい。 引数として、大学生以上の人数、小~高校生の人数、未就学児の人数の受け取るようにし、 返り値が入場料となるようにせよ。 また、[1]Q1では「int(input())」で各人数を入力したと思われるが、 この入力処理をテキスト9.5節「入力に関わる関数(応用)」で紹介したものに書き直せ。
Q1.2 西暦->和暦プログラムの関数化
[1]Q2.1の処理を関数化せよ。引数として西暦を受け取り、和暦を返すようにせよ。 また、テキスト9.5節の階乗を求めるプログラムや素数判定プログラムの例にあるように 処理を一度で終わらせるのではなく、繰り返しプログラムを実行できるようにせよ。 (テキスト9.5節の例だと-1が入力されるまで繰り返すようにしてある)
Q1.3 最大公約数・最小公倍数プログラムの関数化
[2]Q3の処理を関数化せよ。引数として2つの整数を受け取り、それらの最大公約数と最小公倍数を返すようにせよ。
[発展]引数を2つではなく、3つ、あるいは任意の個数(2つ以上)の整数を受け取り、 それらの最大公約数と最小公倍数を返すようにするにはどうすればよいだろうか。 (再帰関数を利用できると上級者という感じですが、繰り返し処理でも書けます。)
Q2. ファイルの解析
8章で取り扱った「sample_data1.txt」のについて 教科ごとに標準偏差を求めよ。 なお、この際には標準偏差を求める関数を定義し、それを各教科に対して実行すると良い。
Q3. 数値微分
1変数で微分可能な関数を定義し、それの数値微分を行いたい。 例えば\(f(x)=x^2+2x\)上の点\((1, 3)\)の接線の傾きは4となるが、これを計算したい。 この例は\(x=1\)の時の接線の傾きの例だが、\(x=-1, 0, 2\cdots\)のときはどうなるのかを計算したい。 さらに関数を\(f(x)=x^2+2x\)に限らず、任意の関数に対して微分を行えるようにしたい。
微分の定義は \begin{align*} \frac{df}{dx}=\lim_{h\to0}\frac{f(x+h)-f(x)}{h} \end{align*} であるが、プログラム言語で理論的な\(h\to0\)を実現することは難しい。 そこで数値微分では\(h\)に十分小さな値を代入することで数値微分を行っている。
1変数で微分可能な関数myfunc(x)を定義し、それを微分する関数mydiff(x)を実装せよ。 なお、\(h\)には\(10^{-6}\)程度を与えると上手くいくことが多く、この\(h\)はmydiffのデフォルト値として与えるようにせよ。
[5] 総合演習
Q1. 暗算速度ゲーム
2x2桁の暗算力を鍛えるゲームとして、以下コードで動くゲームを作成した。
import random # ランダムな数値取得用
import time # 時間計測用
print('2桁x2桁の暗算を3問正解するまでの時間を計測')
cnt = 0 # 正解数カウンター
now_time = time.perf_counter() # 基準タイム
# 3回正解するのでループ
while cnt < 3:
# 2桁の乱数(整数)生成
a = random.randint(10, 99)
b = random.randint(10, 99)
# 回答入力
ans = int(input('{} x {} = '.format(a, b)))
if a*b == ans: # 正誤判定
print('正解\n')
cnt += 1 # カウンタを加算
else:
print('不正解:{}\n'.format(a*b))
# クリアタイム計算
clear_time = time.perf_counter() - now_time
print('クリア時間:{:.2f}'.format(clear_time))
上記コードを改良し、機能を追加したいきたい。
Q1.1 エラーの回避
13行目のinput()は整数しか受け付けない為、文字列などが入力された場合は処理が止まってしまう。 これを回避するにはどうしたらよいだろうか。
Q1.2 [追加]ゲームの開始合図と連続プレイ機能
元のコードでは、コマンドで「python xxxx.py」と入力した直後にゲームが開始される。 プレイヤーの準備がまだ出来ていない可能性もあるので、ゲーム開始前に入力処理を入れたい。 例えば、「開始するなら1を入力>」などと表示・入力処理を行い、 1が入力されたらゲームが開始(時間の測定が開始)されるようにせよ。
また、元のコードでは1回のプレイしか想定しておらず、続けてゲームを行うにはゲーム終了後、 コマンドプロンプトに「python xxxx.py」と再び入力する必要があり手間が掛かる。 例えば、「終了するなら-1を入力>」などと表示・入力処理を行い、連続でプレイできるようにせよ。
Q1.3 [追加]保存機能
元のコードではクリアタイムを表示してゲームを終了するが、クリアタイムをファイルに保存する処理を追加したい。 クリアタイムを保存する機能を付けたせ。 保存ファイルの形式は問わない。
Q1.4 [追加]過去記録との比較機能
Q1.3で作成したファイルを読み込み、 今回のクリアタイムが過去の自己記録と比較して何番目に速いタイムであったのかを表示するようにしたい。 また、過去の記録のベスト3を表示させる機能も欲しい。(ベスト3の表示処理は面倒かもしれない)
Q1.5 [発展]暗算桁数と問題数の変更機能
元コードでは2桁同士の掛け算を3問だが、これを任意に変更できるようにせよ。 ゲーム起動時に桁数と問題数をinput()で受け付けるようにしたい。 さらに言えば、演算を掛け算に限る必要はなく、 足し算や割り算、割り算(商と余りを考慮するから面倒かもしれない)の暗算速度を測れるようにしても良いだろう。 これも例えばinput()で'+'、'-'、'*'、'/'などを入力させ、それに応じた演算のゲームができるようにしても面白いだろう。
Q2. ファイルの振り分け・整理
フォルダの中に「A_02_X.txt」、「A_23_Z.txt」、「B_14_Y.txt」などのファイル名が存在する場合を考える。 これを先頭のアルファベットや次の数値によってフォルダ分けしたい。 ファイルの一覧を取得するには標準ライブラリ「glob」を用いるとよい。 また、ファイルの移動、コピーには「os」や「shutil」ライブラリが便利である。
実用上はカメラで撮った写真などを作成月ごとに振り分けるなどで利用できるだろうが、画像ファイルはメモリ容量の関係上、 配布に向かないのでここでは空のtxtファイルを分類することを考える。 分類のターゲットフォルダは「orizinal.zip」をダウンロードし、展開して利用せよ。
Q2.1 先頭アルファベットによる分類
これらのファイルを先頭のアルファベットごとに「フォルダA」、「フォルダB」に振り分けたい。
Q2.2 数値による分類
「A_02_X.txt」の02部分に着目し、00~19、20~39、40~59、60~79、80~99の5つに分類し、フォルダ分けしたい。
[6] 外部ライブラリ
Q1. 2原子系の1次元連成運動(matplotlib & Numpy利用)
質量\(M\)と\(m\)が交互にばねに繋がれた系を考えたとき、分散関係は以下で与えられる。 \begin{align*} {\omega(k)}^2=\frac{f}{Mm}\left\{(M+m)\pm\sqrt{(M+m)^2-4Mm\sin^2ka}\right\}. \end{align*} ここで\(f\)はばね定数、\(k\)は波数、\(a\)は原子間距離である。 また、質量比として\(\alpha\)を導入し、\(M=\alpha m\)を代入すれば \begin{align*} {\omega(k)}^2&=\frac{f}{\alpha m^2}\left\{m(1+\alpha)\pm\sqrt{m^2(1+\alpha)^2-4\alpha m^2\sin^2ka}\right\}\\ &=\frac{f}{\alpha m}\left\{(1+\alpha)\pm\sqrt{(1+\alpha)^2-4\alpha\sin^2ka}\right\} \end{align*} を得る。プロットする為に無次元化(\(f=1, m=1,a=1\))すれば、 \(\omega_\alpha^+(k)\)と\(\omega_\alpha^-(k)\)は、(\(\omega_\alpha^+(k)\geq\omega_\alpha^-(k)\)) \begin{align*} {\omega_\alpha^+(k)}^2=\frac{1}{\alpha}\left\{(1+\alpha)+\sqrt{(1+\alpha)^2-4\alpha\sin^2k}\right\},\quad {\omega_\alpha^-(k)}^2=\frac{1}{\alpha}\left\{(1+\alpha)-\sqrt{(1+\alpha)^2-4\alpha\sin^2k}\right\} \end{align*} と表せる。
縦軸に振動数\(\omega\)、横軸に波数\(k\)として上記関数をグラフ化し、光学ブランチと音響ブランチの形を可視化せよ。 また、\(\alpha\)の値によってグラフの形がどのように変わるのかを確認せよ。 (\(\alpha=1\)のときは光学ブランチ\(\omega_1^+(k)\)と音響ブランチ\(\omega_1^-(k)\)が\(k=\pm\pi/2\)で交わる。)
※実装上は、波数と質量比を引数に持ち、振動数を返す関数を定義してあげると良いだろう。 なお、上記式の\(\omega\)は2乗されたものであるから、Numpyのsqrt()関数で平方根を取るようするとよい。 なお、sqrt(x)は(x)**(1/2)と同じ結果を返す。
グラフのスタイルは各自に任せるが、私だったらこんな感じにするというサンプルを下記に載せておく。
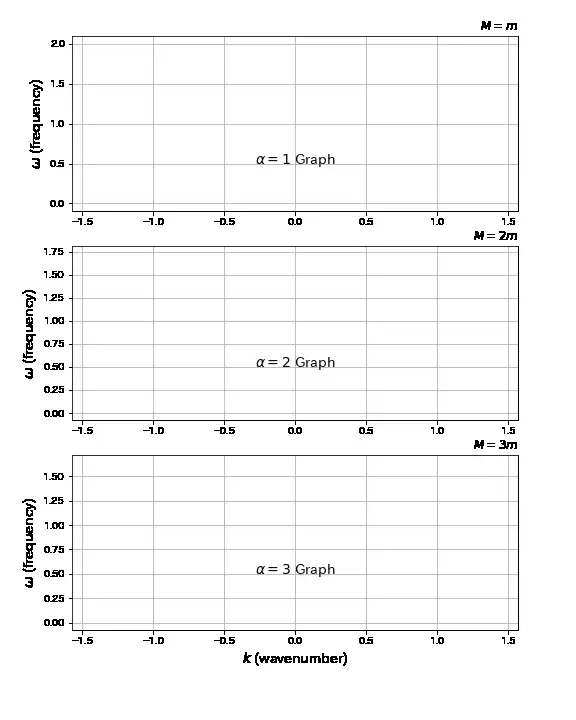
スタイル例
Q2. フェルミ分布関数とボーズ分布関数(matplotlib & Numpy利用)
フェルミ分布関数とボーズ分布関数は以下で与えられる。 \begin{align*} f_{\rm Fermi}(\epsilon) = \frac{1}{\exp\left(\frac{\epsilon-\mu}{k_BT}\right)+1},\quad f_{\rm Bose}(\epsilon) = \frac{1}{\exp\left(\frac{\epsilon-\mu}{k_BT}\right)-1}, \end{align*} この2つの関数を縦軸に\(f\)、横軸に\(\epsilon\)を取りプロットせよ。 また、温度によってグラフの形がどのように変わるのかを確認せよ。